프로그래머스의 문제, "사칙연산"을 풀어보자.
"사칙연산" 문제에서 기본 예시로 주어진 값들을 살펴보면 1 - 3 + 5 - 8 을 계산할 때 아래와 같은 케이스가 나타날 수 있다고 설명하고 있다.
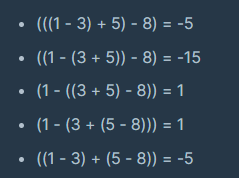
1. 연산 규칙 확인
여기에서 주의해야 할 점은 1 + (-3 + 5) -8 과 같은 연산이 없다는 것이다.
"-" 연산자를 괄호 안에 넣고 그 앞을 "+" 로 치환해주는 식의 연산은 할 수 없다는 것이다.
2. "-" 부호의 특징 인지
일반적으로 "+" 부호만 있다고 생각하면 다 더하는 것이 최대값이다.
그러나 이번 문제에는 "-" 부호가 존재하기 때문에 "-" 연산자의 특징에 대해서 생각해 볼 필요가 있다.
"-" 연산자가 있는데 최대 값을 구하려면 어떻게 해야할까?
바로 "-" 연산자 뒤에 있는 값들을 최소값으로 만들어주는 방식이 필요하다.
위 두가지 규칙을 인지하고 문제를 풀어보도록 하자.
3. 문제 풀이
문제를 풀 때 i, j, d, k 라는 변수가 등장한다. 각각의 뜻은 다음과 같다.
i: 피연산자 시작 인덱스
j: 피연산자 끝 인덱스
d: i와 j의 차이
k: 추가되는 연산자의 인덱스
예를 들어 d=2 , i = 0, j = 2, k=1 값이 있다고 한다면
d=2 : 2개의 인덱스가 떨어진 곳 까지 괄호를 치겠다.
i=0 : 괄호를 치는 시작 인덱스는 0
i=2 : 괄호가 닫히는 마지막 인덱스는 2
k=1:
문제를 해결할 때 연산자와 피연산자를 분리해서 괄호를 씌워보자.
1. 자기 자신만 괄호를 씌운다.
- d=0 , i = 0, j = 0
- (1) - 3 + 5 - 8
- d=0 , i = 1, j = 1
- 1 - (3) + 5 - 8
- d=0 , i = 2, j = 2
- 1 - 3 + (5) - 8
- d=0 , i = 3, j = 3
- 1 - 3 + 5 - (8)
| 1 | |||
| 3 | |||
| 5 | |||
| 8 |
2. 자신 바로 옆에 있는 수까지 괄호를 씌운다.
- d=1 , i = 0, j = 1, k=0
- (1 - 3) + 5 - 8
- 연산자 "-"가 처음 등장하였으며, 연산자의 인덱스는 0이다. (k = 0)
- d=1 , i = 1, j = 2, k=1
- 1 - (3 + 5) - 8
- d=1 , i = 2, j = 3, k=2
- 1 - 3 + (5 - 8)
| 1 | -2 | ||
| 3 | 8 | ||
| 5 | -3 | ||
| 8 |
3. 자신과 두칸 떨어져 있는 수 까지 괄호를 씌운다.
여기서 새로운 케이스인 최대 값과 최소 값이 나타나는 것을 확인할 수 있다.
- d=2 , i = 0, j = 2, k=1
- ((1 - 3) + 5) - 8
- d=2 , i = 0, j = 2, k=0
- (1 - (3 + 5)) - 8
- d=2 , i = 1, j = 3, k=2
- 1 - ((3 + 5) - 8)
- d=2 , i = 1, j = 3, k=1
- 1 - (3 + (5 - 8))
| 1 | -2 | 3, -7 | |
| 3 | 8 | 0, 0 | |
| 5 | -3 | ||
| -8 |
4. 자신과 세 칸 떨어져 있는 수 까지 괄호를 씌운다.
- d=3, i = 0, j = 3, k=2
- (((1 - 3) + 5) - 8)
- ((1 - (3 + 5)) - 8)
- 새로 추가된 연산자는 "-"이다.
- 최대값을 구하기 위해서는 앞쪽 피연산자는 최대값을 가져오고 뒤쪽 피연산자는 최소값을 가져오면 되니 max([i][k]) + min([k+1][j]) 로 계산하면 된다.
- max[0][2] + min[3][3] = 3 - 8 = -5
- d=3, i = 0, j = 3, k=1
- ((1 - 3) + (5 - 8))
- 새로 추가된 연산자는 "+"이다.
- 최대값을 구하기 위해서는 앞쪽 피연산자는 최대값을 가져오고 뒤쪽 피연산자도 최대값을 가지고 오면 되니 max[i][k] + max[k+1][j]로 계산하면 된다.
- max[0][1] + max[2][3] = -2 + -3 = -5
- d=3, i = 0, j = 3, k=0
- (1 - (3 + (5 - 8)))
- (1 - ((3 + 5) - 8))
- 새로 추가된 연산자는 "-"이다.
- 최대값을 구하기 위해서는 앞쪽 피연산자는 최대값을 가져오고 뒤쪽 피연산자는 최소값을 가져오면 되니 max([i][k]) + min([k+1][j]) 로 계산하면 된다.
- max[0][0] + min[1][3] = 1 + 0 = 1
| 1 | -2 | 3. -7 | 1 |
| 3 | 8 | 0, 0 | |
| 5 | -3 | ||
| 8 |
4. 전체 코드
public class p1843 {
public static int solution(String arr[]) {
int size = arr.length / 2 + 1;
char[] operations = new char[size - 1];
int[] numbers = new int[size];
int[][] max = new int[size][size];
int[][] min = new int[size][size];
initArray(min, max, size);
setNumbersAndOperations(arr, numbers, operations);
for (int d = 0; d < numbers.length; d++) {
for (int i = 0; i < numbers.length - d; i++) {
int j = i + d;
if (i == j) {
max[i][j] = numbers[i];
min[i][j] = numbers[i];
continue;
}
for (int k = i; k < j; k++) {
calculate(operations, max, min, i, j, k);
}
}
}
return max[0][numbers.length - 1];
}
private static void calculate(char[] operations, int[][] max, int[][] min, int i, int j, int k) {
// 연산자가 플러스인 경우
if (isPlus(operations[k])) {
max[i][j] = Math.max(max[i][j], max[i][k] + max[k + 1][j]);
min[i][j] = Math.min(min[i][j], min[i][k] + min[k + 1][j]);
return;
}
// 연산자가 마이너스인 경우
max[i][j] = Math.max(max[i][j], max[i][k] - min[k + 1][j]);
min[i][j] = Math.max(min[i][j], min[i][k] - max[k + 1][j]);
}
private static boolean isPlus(char operation) {
return operation == '+';
}
private static void initArray(int[][] min, int[][] max, int size) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
max[i][j] = Integer.MIN_VALUE;
min[i][j] = Integer.MAX_VALUE;
}
}
}
private static void setNumbersAndOperations(String[] arr, int[] numbers, char[] operations) {
for (int i = 0; i < arr.length; i++) {
// 홀수면 피연산자
if (i % 2 == 0) {
numbers[i / 2] = Integer.parseInt(arr[i]);
} else { // 짝수면 연산자
operations[i / 2] = arr[i].charAt(0);
}
}
}
public static void main(String[] args) {
// String[] arr = {"1", "-", "3", "+", "5", "-", "8"};
String[] arr = {"1", "-", "3", "-", "5", "-", "8"};
System.out.println(solution(arr));
}
}