트리란?
사이클이 없는, 연결된 구조
정점의 개수 (vertex, node) : n개
간선의 개수 (edge) : n-1개

정점의 개수가 n개
간선의 개수가 n-1개 라고 트리인 것은 아니다.

트리의 유형 1 ( 루트가 있는 트리 )

1번을 루트로 가정하자 (루트는 마음대로 정할 수 있다.)
parent - child 관계로 묶을 수 있다.
형제으이 관계도 있다. (2 - 3은 형제, 4 - 5는 형제, 6 - 7은 형제)
깊이
루트에서의 거리

깊이의 정의는 0부터 시작할 수 있고, 1부터 시작할 수도 있다.
문제마다 다를 수 있는 부분이다.
조상과 자손

2의 조상은 2, 1
2의 자손은 2, 4, 5
조상과 자손은 parent, child와 달리 자기자신을 포함한다.
이진 트리
자식을 최대 2개만 가지고 있는 트리
포화 이진 트리
리프 노드를 제외한 노드의 자시그이 수: 2
리프 노드의 자식의 수: 0
포화 이진 트리의 노드의 수는 깊이가 h일 때 (2의 h승 - 1)이다.
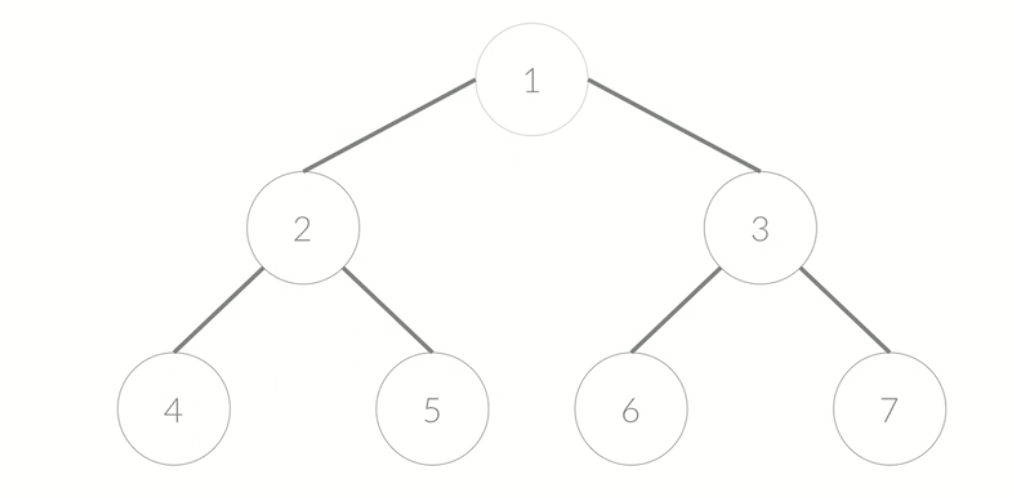
완전 이진 트리
리프 노드를 제외한 노드의 자시그이 수: 2
리프 노드의 자식의 수: 0
마지막 레벨에는 노드가 일부는 없을 수 있음.
오른쪽에서부터 몇 개가 사라진 형태

트리의 표현

모든 노드는 부모를 가지고 있고 부모가 없는 건 루트 뿐이다.
루트의 부모는 0으로 지정해주면 된다.
부모는 한번에 찾을 수 있지만 자식을 찾는데는 시간이 걸린다.
완전 이진 트리에서의 배열의 표현

완전 이진 트리의 경우에는 배열로 표현할 수 있다. 이것이 가장 효율적이다.
클래스를 이용한 표현
클래스를 이용하여 트리를 표현할 수도 있다.

트리의 순회
트리의 모든 노드를 방문하는 순서이다.
그래프의 경우에는 DFS와 BFS가 있었다.
트리에서도 위의 두 방법을 사용할 수 있다.
DFS는 아래와 같이 3가지 출력 순서가 있다.
프리오더
인오더
포스트오더

프리오더 (A -> B -> D -> E -> C -> F -> G)
dfs의 방문하는 것과 동일하다.
자식이 부모의 값을 사용할 때 프리오더를 사용한다.
노드 방문
왼쪽 자식 노드를 루트로 하는 서브 트리 인 오더
오른쪽 자식 노드를 루트로 하는 서브 트리 인 오더
인오더 (D -> B -> E -> A -> F -> C -> G)
일반적으로 잘 사용하지 않는다. 이진 트리에서만 가능
왼쪽 자식 노드를 루트로 하는 서브 트리 인 오더
노드 방문
오른쪽 자식 노드를 루트로 하는 서브 트리 인 오더
포스트오더 (D -> E -> B -> F -> G -> C -> A)
가장 많이 사용 ( 자식에 대한 정보를 이용하여 현재 노드를 계산할 때 포스트오더를 사용한다.)
왼쪽 자식 노드를 루트로 하는 서브 트리 인 오더
오른쪽 자식 노드를 루트로 하는 서브 트리 인 오더
노드 방문
백준 트리 순회 문제를 풀어보자